FS-CES (Finite State - Chaotic Encryption System)
Cryptographic Techniques Specifications
In information-theoretical point of view, chaotic dynamical systems
are those systems in which information is lost along orbits. Chaotic
cryptosystems may develop in the future since their security and
specification standards can be evaluated by dynamical system
theory. FS-CES obtains a ciphertext by applying a modification of the
one-dimensional skew tent map fa to a plaintext. We can derive
fa by moving the critical point (a) of the tent map away from
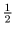 ;
a is used as secret key. Intuitively, we would like
to let fan(x) (n is a sufficiently large integer) be the
ciphertext corresponding to a plaintext
;
a is used as secret key. Intuitively, we would like
to let fan(x) (n is a sufficiently large integer) be the
ciphertext corresponding to a plaintext
![$x\in [0,1]$](specification-img2.png) .
However,
decryption uniqueness would be lost in this configuration since fais two-to-one. To overcome this improperness, we discretize the plaintext
space, the ciphertext space, the key space, and the transformation,
constructing a one-to-one map explicitly. The modified map is explicitly
written by rounding, and computation time does not
remarkably increase compared with the original skew tent map.
.
However,
decryption uniqueness would be lost in this configuration since fais two-to-one. To overcome this improperness, we discretize the plaintext
space, the ciphertext space, the key space, and the transformation,
constructing a one-to-one map explicitly. The modified map is explicitly
written by rounding, and computation time does not
remarkably increase compared with the original skew tent map.
We have further analyzed its security using dynamical system theory
(see Self Evaluation Reports), and cryptological strength has been assured
based on information theory. The iteration number is determined by these
investigations.
For simplicity, we stretch the domain and the range of the skew tent
map from [0,1] to [0,M]. We denote this rescaled skew tent map by
FA. The integer
M = 2128 is equal to the cardinality of the
plaintext space
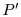 ,
the ciphertext space
,
the ciphertext space
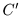 ,
and
the key space
,
and
the key space
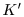 ;
these spaces are defined by
;
these spaces are defined by
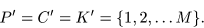 |
(1) |
We define a discretized skew tent map
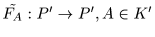 by
by
where 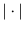 indicates the cardinality of a set.
indicates the cardinality of a set.
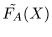 is naturally interpreted as the
ascending order of FA(X) in all
is naturally interpreted as the
ascending order of FA(X) in all
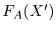 's,
's,
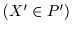 .
If
FA(X1) = FA(X2), X1 < A < X2, then we define
.
If
FA(X1) = FA(X2), X1 < A < X2, then we define
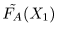 and
and
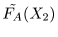 so that
so that
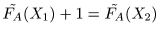 .
.
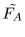 is a one-to-one mapping on
is a one-to-one mapping on
 .
.
FS-CES is defined by the encryptor
and the decryptor
The corresponding formulae are as follows:
where
Round-of and round-up are denoted by
 ,
,
 ,
respectively.
A key should satisfy
0.4M < A < 0.6M.
If A were very far from 0.5M, information dissipation is slow per
iteration, and consequently large n would be required.
The security analysis below assumes this restriction.
,
respectively.
A key should satisfy
0.4M < A < 0.6M.
If A were very far from 0.5M, information dissipation is slow per
iteration, and consequently large n would be required.
The security analysis below assumes this restriction.
A key should not be too close to A = 0.5M (avoid A such that
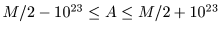 ). The encryption functions for
). The encryption functions for
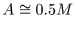 would have structures similar to that of the shift
map. Attackers might exploit this similarity.
would have structures similar to that of the shift
map. Attackers might exploit this similarity.
Iteration number n should be larger than
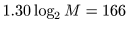 .
This
requirement is on the basis of our security analysis
(see Self Evaluation Reports).
.
This
requirement is on the basis of our security analysis
(see Self Evaluation Reports).
Questions or comments regarding this service?
Contact us.
Copyright (C) 2000 R&D Team, AIHARA Electrical Engineering Co., Ltd.
All rights reserved.
![]() by
by
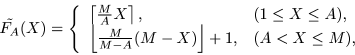
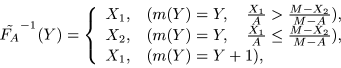
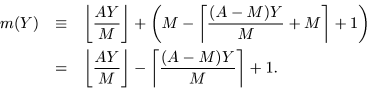
![]() ). The encryption functions for
). The encryption functions for
![]() would have structures similar to that of the shift
map. Attackers might exploit this similarity.
would have structures similar to that of the shift
map. Attackers might exploit this similarity.
![]() .
This
requirement is on the basis of our security analysis
(see Self Evaluation Reports).
.
This
requirement is on the basis of our security analysis
(see Self Evaluation Reports).