Previous: Introduction Next: Security Analysis Up: FS-CES

  
Specifications for FS-CES

We use a skew tent map f_a (Fig. 1) as a basic map. We can derive f_a by moving the critical point (a) of the tent map away from $\frac{1}{2}$; a is used as secret key. The Lyapunov exponent of f_a is $\lambda = -a\log a -(1-a)\log (1-a)$.

  

Figure 1: The skew tent map: x_n+1 = f_a(x_n)

Intuitively, we would like to let f_aⁿ(x) (n is a sufficiently large integer) be the ciphertext corresponding to a plaintext $x\in [0,1]$. However, decryption uniqueness would be lost in this configuration since f_ais two-to-one. To overcome this improperness, we discretize the plaintext space, the ciphertext space, the key space, and the transformation, constructing a one-to-one map explicitly.

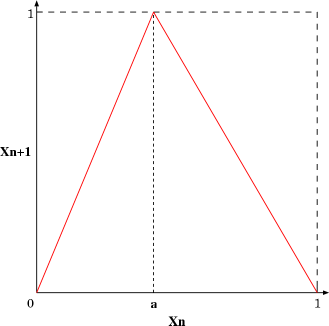
For simplicity, we stretch the domain and the range of the skew tent map from [0,1] to [0,M]. We denote this rescaled skew tent map by F_A. The integer M = 2¹²⁸ is equal to the cardinality of the plaintext space $P^{\prime}$, the ciphertext space $C^{\prime}$, and the key space $K^{\prime}$; these spaces are defined by

$$P^{\prime} = C^{\prime} = K^{\prime} = \{ 1, 2, \ldots M\}.$$ (1)

Next, let us consider the conditions for a discretized skew tent map to satisfy (see Fig. 2). The black points on the x axis is the points in $P^{\prime}$. If we set F_A(X) as the state after transforming $X\in P^{\prime}$, there would arise two inconsistencies: a point from the left and another point from the right would possibly collide after transformation, and generally speaking, $F_A(X)\notin P^{\prime}$. Accordingly, we define a discretized skew tent map $\tilde{F_A}: P^{\prime} \to P^{\prime}, A\in K^{\prime}$ as follows:

$$\tilde{F_A}(X) \equiv \left\vert \{ X^{\prime}\in P^{\prime} \vert F_A(X^{\prime}) < F_A(X)) \} \right\vert +1$$

where $\vert\cdot \vert$ is cardinality of a set. $\tilde{F_A}(X)$ is the ascending order of F_A(X)among all $F_A(X^{\prime})$'s $(X^{\prime} \in P^{\prime})$.

X is transformed into the number of black points in the region enclosed with the two circles in Fig. 2.

If F_A(X₁) = F_A(X₂), X₁ < A < X₂, then we define $\tilde{F_A}(X_1)$ and $\tilde{F_A}(X_2)$ so that $\tilde{F_A}(X_1) + 1 = \tilde{F_A}(X_2)$. $\tilde{F_A}$ is one-to-one mapping on $P^{\prime}$.

  

Figure: The discretized skew tent map: $\tilde{F_A}$

FS-CES is defined by the encryptor

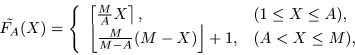
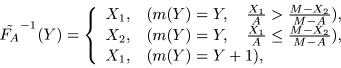
$$e_A : P^{\prime} \to C^{\prime},\quad e_A(X) = \tilde{F_A}^n (X),$$

and the decryptor

$$d_A : C^{\prime} \to P^{\prime},\quad d_A(X) = \tilde{F_A}^{-n}(X).$$

The corresponding formulae are as follows:

$$\tilde{F_A}(X) =\left\{ \begin{array}{ll} \left\lceil \frac{M... ...M - X) \right\rfloor + 1, & (A < X \le M), \end{array}\right.$$

$$\tilde{F_A}^{-1}(Y) = \left\{ \begin{array}{ll} X_1, & (m(Y) ... ...c{M - X_2}{M - A}),\\ X_1, & (m(Y) = Y+1), \end{array}\right.$$

where

$$\begin{eqnarray*}m(Y) &\equiv& \left\lfloor \frac{AY}{M} \right\rfloor - \left\lceil \frac{(A-M)Y}{M} \right\rceil + 1. \end{eqnarray*}$$

Round-off and round-up are denoted by $\lfloor \rfloor$, $\lceil \rceil$, respectively. Table 1 shows the encryption process. We can observe the exponential diversion of information by $\tilde{F_A}$ keeping the one-to-one correspondence.

  

Table: An example of encryption by $\tilde{F_A}^n$. We set M=373 and A=201. The numbers in the top row denote the iteration number n.

Previous: Introduction Next: Security Analysis Up: FS-CES

Questions or comments regarding this service? Contact us. Copyright (C) 2000 R&D Team, AIHARA Electrical Engineering Co., Ltd.
All rights reserved.